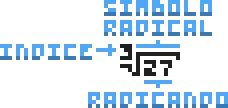Radiciação

Radiciação é uma operação matemática que obtém a raiz de um número, ou seja, um valor que, quando elevado a uma potência igual ao índice, resulta no radicando.

O Básico

$\sqrt[n]{x}$

O $n$ é o índice.
O $x$ é o radicando.
O $\sqrt{}$ é o símbolo radical.

$\sqrt[n]{x}=m \iff m^n=x$

A radiciação é a operação inversa da potenciação com expoente fixo.

$x^{\frac{1}{n}} = \sqrt[n]{x}$

A radiciação pode ser interpretada como uma potenciação com expoente fracionário.

$\sqrt{x} = \sqrt[2]{x}$

Quando o índice não é explícito, o índice é $2$.

Exemplos

$\sqrt{121} = 11$
$\sqrt[3]{125} = 5$
$\sqrt{37} \approx 6.0827$
$\sqrt[3]{89} \approx 4.4647$

Vídeo ensinando radiciação:
https://www.youtube.com/watch?v=ZV4HavJfpII

Raiz Quadrada

$\sqrt{1} = 1~~~\sqrt{4} = 2\\ \sqrt{9} = 3~~~\sqrt{16} = 4\\ \sqrt{25} = 5~~~\sqrt{36} = 6\\ \sqrt{49} = 7~~~\sqrt{64} = 8\\ \sqrt{81} = 9~~~\sqrt{100} = 10$

Raiz Cúbica

$\sqrt[3]{1} = 1~~~\sqrt[3]{8} = 2\\ \sqrt[3]{27} = 3~~~\sqrt[3]{64} = 4\\ \sqrt[3]{125} = 5~~~\sqrt[3]{216} = 6\\ \sqrt[3]{343} = 7~~~\sqrt[3]{512} = 8\\ \sqrt[3]{729} = 9~~~\sqrt[3]{1000} = 10$

Propriedades da Radiciação